This article presents an effort to use Induction in geometry to prove Sylvester Gallois Theorem.
Theorem statement can be viewed here
For the proof, let us rephrase the theorem as follows –
(1) Given a finite set of points in Euclidean space such that any line passing through two of the points passes through at least one more of them, all points have to be collinear.
Proof
Let n be the finite number of points in the given set.
Base case:
Let n=3,
Given 3 points, such that a line containing two of them passes through one more of them, they are by definition, collinear.
Thus (1) is true for n=3.
Induction step
P(k) :
Let (1) be true for a given k points set.
P(k+1):
For an external point in the same space to pass through any line passing through two of the points in the k-points set in P(k), it has to pass through the line passing through all of them.
Thus the only way to expand the given set of k points to a set of k+1 number of points, is to include an external point which is collinear with the existing points.
Hence all k+1 points of the expanded set are collinear.
Thus if (1) is true for n=k, then it is true for n=k+1
Thus by principle of induction, (1) is true for all n>=3.
Intuitive right? but the proof doesn’t hold.
Why doesn’t the proof hold?
The proof doesn’t hold because the method of progression applied is too unidirectional to cover the variations in the euclidean space. The insufficiency can be proven by the counter proofs which employ the same method – this time to prove some absurd theories which can be disproven easily by employing other methods.
Two such counter proofs were provided, one by my colleague Harsh Kohli and other by my brother Vishnu K.S.
I’m providing Vishnu’s proof here which is similar to the above and hence simpler within this context.
The Counter Proof
Consider the set below set of line segments:
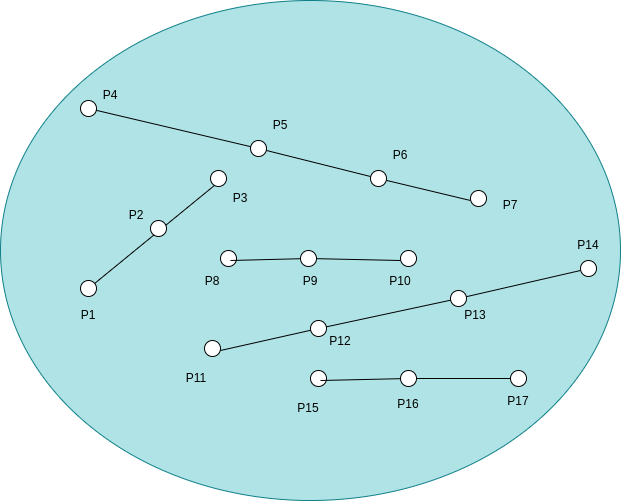
We see a bunch of line segments, with few defined points on them, and NOT following any concurrency.
Now let’s define an absurd theory about these points which obviously doesn’t hold.
The theory is: “Given a finite set of points in Euclidean space such that any point passes through a line segment having two more of them, all points have to be collinear.
Clearly, as shown in the above set, each point there passes through a line segment having two more of them, and all of them put together are not collinear.
Now the above method of progression can be used to prove this wrong theory as true. (obvious and simple proof as above and and hence not repeating)
Overall this has been a exercise which helped me have some great interaction with similar minds, including few math professors in the academia. Keeping the approach documented here hence.
Kj [/.] Sreekumar programs computers as a hobby and profession. Into programming from his school days, Sree uses Codemarvels to key in facts and fixes he finds interesting while working on different projects. Some of the articles here give away a few shades of his philosophical leanings too.

